THIRD SUMMATIVE EVALUATION
CLASS 5 (V) WBBSE
MATH QUESTION PAPER
Class 5 Math 3rd Unit Test Question Paper Set-3 wbbse | পঞ্চম শ্রেণি গণিত তৃতীয় ইউনিট টেস্ট প্রশ্নপত্র সেট-৩
📌পঞ্চম শ্রেণি ইউনিট টেস্ট প্রশ্নপত্র Click Here
Set-3
তৃতীয় পর্যায়ক্রমিক মূল্যায়ন
পঞ্চম শ্রেণি
বিষয় : গণিত
পূর্ণমান : ৫০ সময় : ১.৩০ মিনিট
‘ক’ - বিভাগ (পাটীগণিত)
১। সঠিক উত্তরটি নির্বাচন করে লেখো (যে কোনো চারটি) : ১×৪=৪
(ক) দুই অঙ্কের বৃহত্তম ও ক্ষুদ্রতম সংখ্যার পার্থক্য (৯৯ / ১০/ ৮৯ / ৭৯)।
উত্তরঃ ৮৯. (বৃহত্তম দুই অঙ্কের সংখ্যা ৯৯, ক্ষুদ্রতম ১০; ৯৯−১০ = ৮৯)
(খ) ৩ এবং ৯-এর ল.সা.গু ও গ.সা.গু-র গুণফল (৩ / ৯ / ২৭ / ৩০)।
উত্তরঃ ২৭
(গ) `frac১(৪)` + `frac১(৪)` + `frac১(৪)` + `frac১(৪)` + `frac১(৪)` এর মান (`frac১(৪)` / `frac৩(৪)` / ১ / `frac৫(৪)`)
উত্তরঃ `frac৫(৪)`
(ঘ) একটি বর্গাকার চিত্রের পরিসীমা ২৪ মিটার হলে, তার একটি বাহুর দৈর্ঘ্য (২ মি / ৪ মি / ৬ মি / ৮ মি)।
উত্তরঃ ৬ মি
(ঙ) ১.২৫-কে ভগ্নাংশে পরিণত করলে সেটি একটি (প্রকৃত ভগ্নাংশ / অপ্রকৃত ভগ্নাংশ / মিশ্র ভগ্নাংশ / কোনোটিই নয়)।
উত্তরঃ অপ্রকৃত ভগ্নাংশ।
(চ) ৯টি পেনের দাম ৪৫ টাকা হলে ১০টি পেনের দাম হবে (৪০ টাকা / ৫০ টাকা / ৩০ টাকা / ৬০ টাকা)।
উত্তরঃ ৫০ টাকা
২। নিচের প্রশ্নগুলির উত্তর দাও (যে কোনো চারটি) : ২×৪= ৮
(ক) দুটি সংখ্যার গুণফল ১০৩৫, একটি সংখ্যা ২৩ হলে অন্যটি কত ?
সমাধান :
দুটি সংখ্যার গুণফল ১০৩৫ একটি সংখ্যা ২৩
অন্য সংখ্যা = (১০৩৫ ÷ ২৩) = ৪৫ (উত্তর)
(খ) সিরাজ বাগানের `frac৬(১৭)` অংশে ফুলের চারা লাগিয়েছে। মণিকা `frac৩(৩৪)` অংশে ফুলের চারা লাগিয়েছে। তারা দুজনে মোট কত অংশে ফুলের চারা লাগিয়েছে ?
সমাধান :
`frac৬(১৭)` + `frac৩(৩৪)`
= `frac{(৬×২)+(৩×১)}{৩৪}`
= `frac(১২+৩){৩৪}`
= `frac(১৫){৩৪}`
∴ সিরাজ ও মনিকা মিলে মোট `frac(১৫){৩৪}` অংশে ফুলের চারা লাগিয়েছে। (উত্তর)
কে বেশি চারা লাগিয়েছে তা জানার জন্যে আমরা `frac৬(১৭)` এবং `frac৩(৩৪)` কে সমহর বিশিষ্ট করে পাই,
`frac৬(১৭)` = `frac(৬×২){১৭×২}` = `frac(১২){৩৪}`
`frac৩(৩৪)` = `frac(৩×১){৩৪×১}` = `frac(৩){৩৪}`
= `frac(১২){৩৪}` > `frac(৩){৩৪}`
∴ সিরাজ বাগানে বেশি ফুলের চারা লাগিয়েছে।
সে কত বেশি লাগিয়েছে তা হল—
`frac(১২){৩৪}` – `frac(৩){৩৪}`
= `frac(১২–৩){৩৪}`
= `frac(৯){৩৪}` অংশ। (উত্তর)
(গ) আয়তাকার মাঠের দৈর্ঘ্য ৫০ মিটার এবং প্রস্থ ৩০ মিটার। মাঠের পরিসীমা কত ? (পৃষ্ঠা সংখ্যা ১২৬)
(ঘ) ৪টি লাঙল দিয়ে কিছু জমি চাষ করতে ৫ দিন সময় লাগে। ১টি লাঙল দিয়ে ঐ জমি চাষ করতে কত দিন সময় লাগবে ? (পৃষ্ঠার সংখ্যা ২০৩)
সমাধান :
গণিতের ভাষায় সমস্যাটি,
| লাঙলের সংখ্যা | সময় |
| ৪ টি | ৫ দিন |
| ১ টি | ? |
কাজের পরিমাণ নির্দিষ্ট থাকলে, লাঙলের সংখ্যা বাড়লে দিনের পরিমাণ কমবে এবং লাঙলের সংখ্যা কমলে, দিনের পরিমাণ বাড়বে। লাঙলের সংখ্যার সঙ্গে দিন সংখ্যার সম্পর্ক বিপরীত।
ঐকিক নিয়মে সমাধান করে পাই,
ঐ নির্দিষ্ট পরিমাণ জমি, ৪ টি লাঙল দিয়ে ৫ দিনে চাষ করা যায়
১ টি লাঙল দিয়ে ৪ × ৫ দিনে চাষ করা যায়
= ২০ দিনে চাষ করা যায়।
∴ ১ টি লাঙল দিয়ে ঐ জমি চাষ করতে ২০ দিন সময় লাগবে। (উত্তর)
(ঙ) সরল করো :
১৬ – [৮ – {৫ – ২ (২ – `\overline{১ – ১}`)}] (পৃষ্ঠা সংখ্যা ১৩৮)
(চ) সানিয়া ১৫০.৫০ টাকায় এক ঝুড়ি আম কিনল। বাজারে গিয়ে ১৭৫ টাকায় তা বিক্রি করে দিল। সে কত টাকা বেশী পেল ? (পৃষ্ঠা সংখ্যা ১৫২)
৩। নীচের প্রশ্নগুলির উত্তর দাও (যে কোনো চারটি) : ৩x৪=১২
(ক) তিনটি ঘণ্টা একসঙ্গে বাজার পর যথাক্রমে ১৫, ২০ ও ২৫ সেকেন্ড অন্তর বাজে। কতক্ষণ পর ঘণ্টাগুলি আবার একসঙ্গে বাজবে ?
সমাধান :
ঘণ্টাগুলি যথাক্রমে ১৫ সেকেন্ড, ২০ সেকেন্ড ও ২৫ সেকেন্ড অন্তর বাজে।
তাহলে এগুলি আবার একসঙ্গে বাজবে তাদের ল.সা.গু (LCM) বের করলে।
তিনটি সংখ্যার ল.সা.গু – ৫×৩×৪×৫=৩০০
সুতরাং ঘণ্টাগুলি আবার একসঙ্গে বাজবে ৩০০ সেকেন্ড পরে (অর্থাৎ ৫ মিনিট পরে)।
(খ) মিহির বাড়ি থেকে স্টেশনে যাওয়ার সময় `frac৭(৮)` অংশ বাসে ও `frac১(১২)` অংশ সাইকেলে গেল। মিহির বাকি অংশ পথ হেঁটে গেল। মিহির কত অংশ পথ হেঁটে গেল ?
সমাধান :
মিহির বাসে ও সাইকেলে গেল, `frac৭(৮)` + `frac১(১২)`
= `frac{(৭×৩)+(১×২)}{২৪}`
= `frac(২১+২){২৪}`
= `frac(২৩){২৪}`
সুতরাং মিহির মোট `frac(২৩){২৪}` অংশ বাসেও সাইকেলে গেল।
ধরি, মোট রাস্তা ১ অংশ
মিহির হেঁটে গেল—
`১ – frac(২৩){২৪}`
= `frac(১){১}–frac(২৩){২৪}`
= `frac{(১×২৪)–(২৩×১)}{২৪}`
= `frac(২৪–২৩){২৪}`
= `frac(১){২৪}` (উত্তর)
(গ) একটি বর্গাকার মাঠের দৈর্ঘ্য ৪০ মিটার। প্রতি বর্গমিটার ৬ টাকা হিসাবে তাতে ঘাস লাগাতে কত খরচ হবে ? (পৃষ্ঠা নং ১২৯)
সমাধানঃ বর্গাকার মাঠের দৈর্ঘ্য ৪০ মিটার ।
∴ বর্গাকার মাঠের ক্ষেত্রফল ৪০×৪০ বর্গ মিটার = ১৬০০ বর্গ মিটার
মোট খরচ = (১৬০০ × ৬) টাকা = ৯৬০০ টাকা
(ঘ) ১ ডজন ডিমের দাম ৪৮ টাকা হলে ১৯ টা ডিমের দাম ঐকিক নিয়মে নির্ণয় করো। (১ ডজন = ১২টি) (পৃষ্ঠা নং ১৯৮)
সমাধান :
গণিতের ভাষায় সমস্যাটি হল—
১ ডজন = ১২ টি
| ডিমের সংখ্যা | ডিমের সংখ্যা |
| ১২ | ৪৮ |
| ১৯ | ? |
ডিমের সংখ্যা বাড়লে ডিমের দামও বাড়বে।
ডিমের সংখ্যা কমলে ডিমের দামও কমবে।
ডিমের সংখ্যার সাথে ডিমের দামের সরল সম্পর্ক।
১২ টি ডিমের দাম ৪৮ টাকা
১ টি ডিমের দাম ৪৮ ÷ ১২ = ৪ টাকা
১৯ টি ডিমের দাম = ১৯ × ৪ = ৭৬ টাকা
∴ ১৯ টা ডিমের দাম ৭৬ টাকা। (উত্তর)
(ঙ) একটি পোলট্রিতে ৪০০০টি মুরগির ২৫০ দিনের খাবার মজুত ছিল। কিন্তু আরো ১০০০টি মুরগি আনা হল। ঐ মজুত খাবারে মুরগিগুলির কতদিন চলবে ? (পৃষ্ঠা নং ২০৭)
সমাধান :
গণিতের ভাষায় সমস্যাটি হল—
| পোলট্রিতে মুরগির সংখ্যা | খাবার মজুত দিন সংখ্যা |
| ৪০০০ | ২৫০ |
| ১০০০+৪০০০ = ৫০০০ | ? |
মুরগির সংখ্যা বাড়লে দিনসংখ্যা কমবে এবং মুরগির সংখ্যা কমলে দিনসংখ্যা বাড়বে।
মুরগির সংখ্যার সঙ্গে খাবার মজুতের দিনসংখ্যার ব্যস্ত সম্পর্ক।
৪০০০ মুরগির খাবার মজুতের দিনসংখ্যা ২৫০ দিন
১ টি মুরগির খাবার মজুতের দিনসংখ্যা ৪০০০ × ২৫০ দিন
৫০০০ টি মুরগির খাবার মজুতের দিনসংখ্যা `frac(৪০০০ × ২৫০){৫০০০}` = ২০০ দিন
∴ ৫০০০ টি মুরগির মজুত খাবারের দিনসংখ্যা ২০০ দিন। (উত্তর)
(চ) সরল করো : ১০×৬ – [৫ + {১০ – (৫ – ২)} ৩] (পৃষ্ঠা নং ১৪০)
সমাধান :
১০×৬ – [৫ + {১০ – (৫ – ২)} ৩]
= ১০×৬ – [৫ + {১০ – ৩)} ৩]
= ১০×৬ – [৫ + ২১]
= ১০ × ৬ – ২৬
= ৬০ – ২৬
= ৩৪ (উত্তর)
‘খ’ বিভাগ
৪। সঠিক উত্তরটি নির্বাচন করে লেখো (চারটি) : ১×৪=৪
(ক) কোনটি আঁকতে সবচেয়ে কম জায়গা লাগবে ? (সরলরেখা / সরলরেখাংশ / কোণ / বিন্দু)।
উত্তরঃ বিন্দু
(খ) তিনটি সমরেখ বিন্দু দিয়ে কতগুলি সরলরেখা আঁকা যায় ? (১টি / ২টি / ৩টি/ অসংখ্য)।
উত্তরঃ ১টি
(গ) সরল কোণটি হল (০° / ৯০° / ৬০° / ১৮০°)।
উত্তরঃ ১৮০°
(ঘ) একটি মুখবন্ধ কৌটার সমতলের সংখ্যা (১টি / ২টি / ৩টি / একটিও না)।
উত্তরঃ ২টি
(ঙ) শঙ্কুর তলদেশ (বৃত্তাকার ক্ষেত্র / ত্রিভুজাকার ক্ষেত্র / বর্গক্ষেত্রাকার / আয়তক্ষেত্রাকার)।
উত্তরঃ বৃত্তাকার ক্ষেত্র।
(চ) সূক্ষ্মকোণী ত্রিভুজের সূক্ষ্মকোণের সংখ্যা (১টি / ২টি / ৩টি / ৪টি)।
উত্তরঃ ৩টি
৫। নিচের প্রশ্নগুলির উত্তর দাও (যে কোনো আটটি) : ২×৮=১৬
(ক) স্কেলের সাহায্যে ৮.৫ সেমি সরলরেখাংশ আঁকো ও তার নাম দাও।
উত্তরঃ
• প্রথমে স্কেলের সাহায্যে ৮.৫ সেমি দৈর্ঘ্যের একটি সরলরেখাংশ আঁকো।
• রেখাংশটির দুই প্রান্তে একটি একটি বিন্দু চিহ্নিত করো।
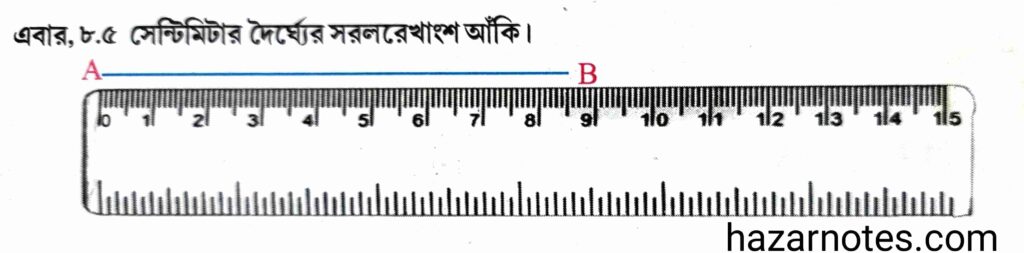
• প্রান্তদ্বয়ের নামকরণ করো, যেমন A ও B।
রেখাংশটির নাম হবে AB এবং এর দৈর্ঘ্য AB = ৮.৫ সেমি।
(খ) স্থূলকোণ কাকে বলে চিত্রসহ লেখো।
উত্তরঃ
স্থূলকোণ : যে কোণের মান ৯০° -এর চেয়ে বড় এবং ১৮০° -এর চেয়ে ছোট তাকে স্থূলকোণ বলে।
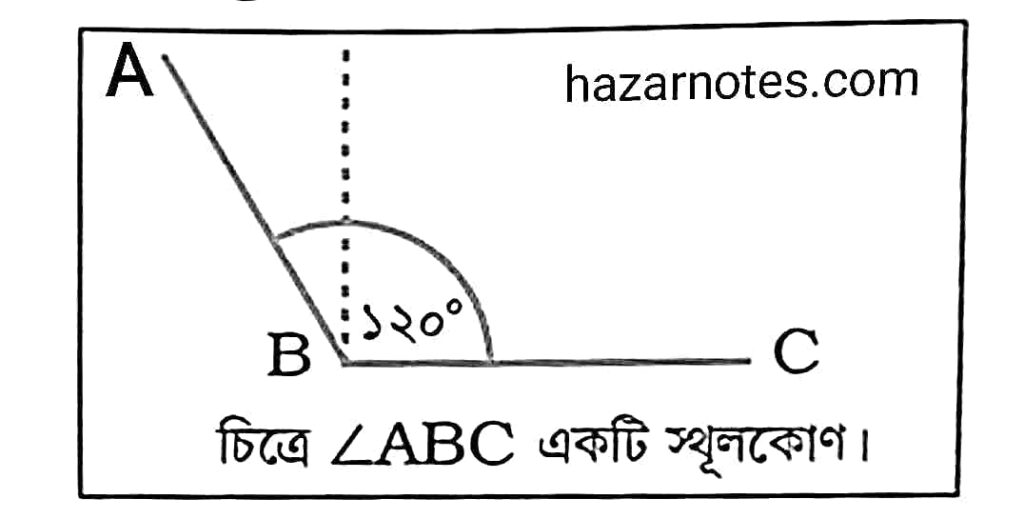
এখানে `angleBAC` একটি স্থূলকোণ কারণ এটি ৯০° -এর চেয়ে বড় কিন্তু ১৮০°-এর চেয়ে ছোট।
(গ) একটি আয়তঘনকের চিত্র আঁকো। একটি উদাহরণ দাও।
উত্তরঃ 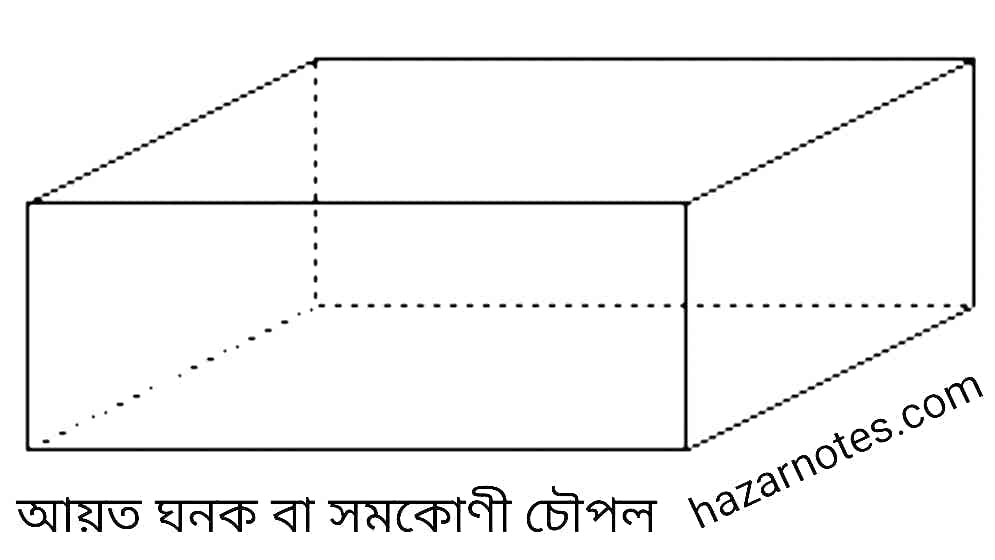
(ঘ) একটি চতুর্ভুজাকার ভূমি বিশিষ্ট পিরামিডের তলসংখ্যা ও ধার সংখ্যা লেখো।
উত্তরঃ তলসংখ্যা—
১টি চতুর্ভুজ ভূমি, ৪টি ত্রিভুজাকার পার্শ্বতল
মোট = ৫টি তল
ধারসংখ্যা— ভূমির চতুর্ভুজের ৪টি ধার, ভূমির প্রতিটি শীর্ষ থেকে শীর্ষবিন্দুতে যাওয়া ৪টি ধার
মোট = ৮টি ধার
(ঙ) চাঁদার সাহায্যে ৭৫° কোণ আঁকো। এটি কী ধরণের কোণ ?
উত্তরঃ নিজে করো।
(চ) ১ সেমি, ৩ সেমি ও ৫ সেমি বাহুবিশিষ্ট ত্রিভুজ আঁকা সম্ভব কী ? যুক্তি দাও।
উত্তরঃ নিজে করো।
(ছ) ১.৫ সেমি ব্যাসার্ধবিশিষ্ট বৃত্ত আঁকো।
উত্তরঃ নিজে করো।
(জ) কোণ ভেদে ত্রিভুজ কয় প্রকার ও কী কী ?
উত্তরঃ কোণভেদে ত্রিভুজ প্রধানত তিন প্রকার: সূক্ষ্মকোণী ত্রিভুজ, সমকোণী ত্রিভুজ, এবং স্থূলকোণী ত্রিভুজ।
(ঝ) বৃত্তাকার মাঠে যখন দৌড় প্রতিযোগীতার জন্য বিভিন্ন লাইন করা হয় তখন বাইরের প্রতিযোগী আগে দাঁড়ায় আর ভেতরের প্রতিযোগী পিছনে দাঁড়ায় কেন ?
উত্তরঃ কারণ—
(i) বৃত্তাকার ট্র্যাকের বাইরের লেনের দৈর্ঘ্য ভেতরের লেনের চেয়ে বেশি।
(ii) যদি সব প্রতিযোগী একই লাইন থেকে শুরু করত, তাহলে বাইরের লেনের প্রতিযোগীকে বেশি পথ পাড়ি দিতে হতো।
(iii) তাই বাইরের লেনের প্রতিযোগীকে সামনের দিকে সরানো হয়, যাতে সকল প্রতিযোগী একই দূরত্বে দৌড় শেষ করতে পারে।
সারসংক্ষেপ : সবার জন্য সমান দৌড়দূরত্ব নিশ্চিত করতে বাইরের লেনের প্রতিযোগীকে সামনে রাখা হয়।
(ঞ) একটি সমকোণী ত্রিভুজ আঁকো। এর কটি সূক্ষ্মকোণ ?
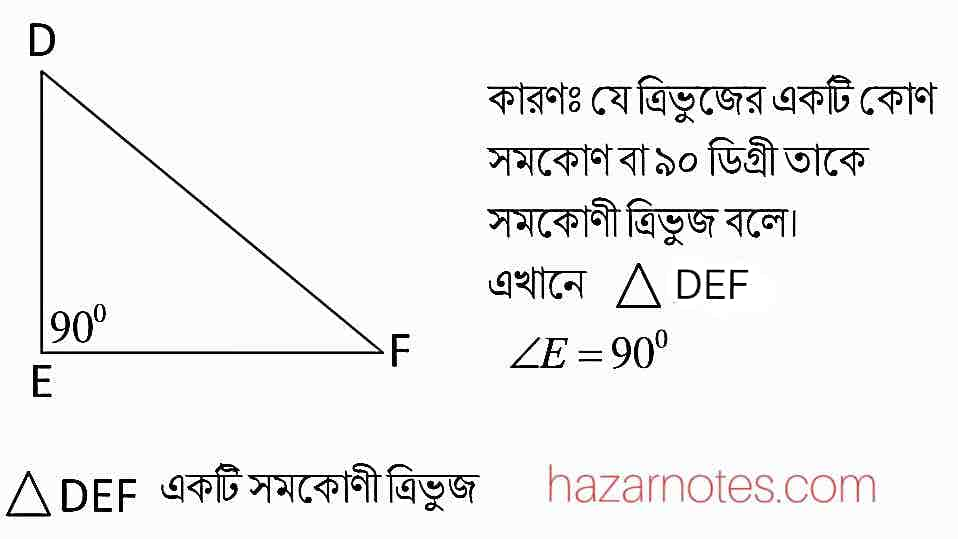
৬। যে কোনো একটি প্রশ্নের উত্তর দাও : ৪
(ক) দুটি সুষম বস্তুর উদাহরণ চিত্রসহ লেখো। প্রতি ক্ষেত্রে বস্তুর তলসংখ্যা কত হবে লেখো। ২+২
উত্তরঃ দুটি সুষম বস্তুর উদাহরণ হল সুসম পিরামিড বা চতুস্তলক ও সুষম ঘনক।
(i) সুষম চতুস্তলক—
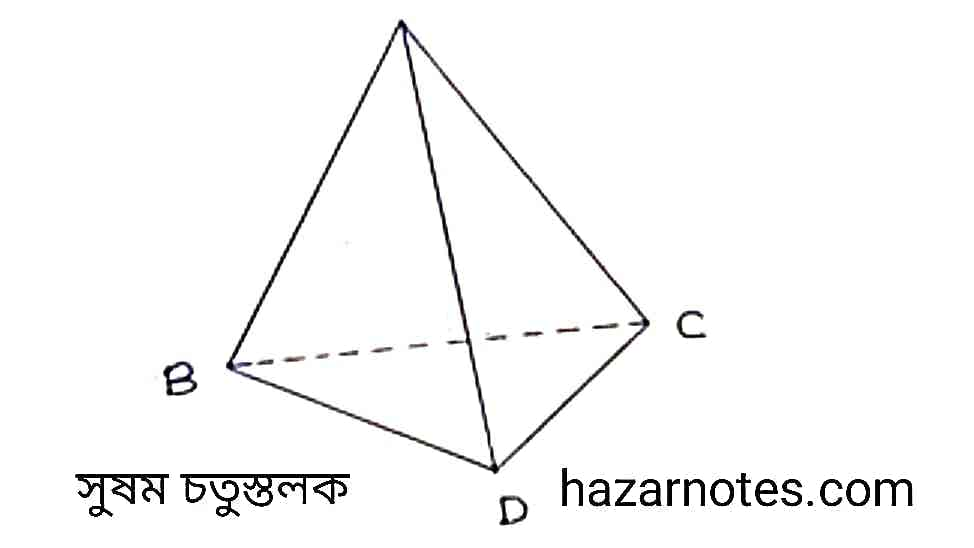
চিত্র : একটি সুষম চতুস্তলকের চারটি তলই সমান আকারের সমবাহু ত্রিভুজ দ্বারা গঠিত।
সুষমতা : এর প্রতিটি তল একটি সুষম ত্রিভুজ এবং এর প্রতিটি শীর্ষবিন্দুতে তিনটি তল মিলিত হয়।
তলসংখ্যা : ৪টি।
(ii) সুষম ঘনক
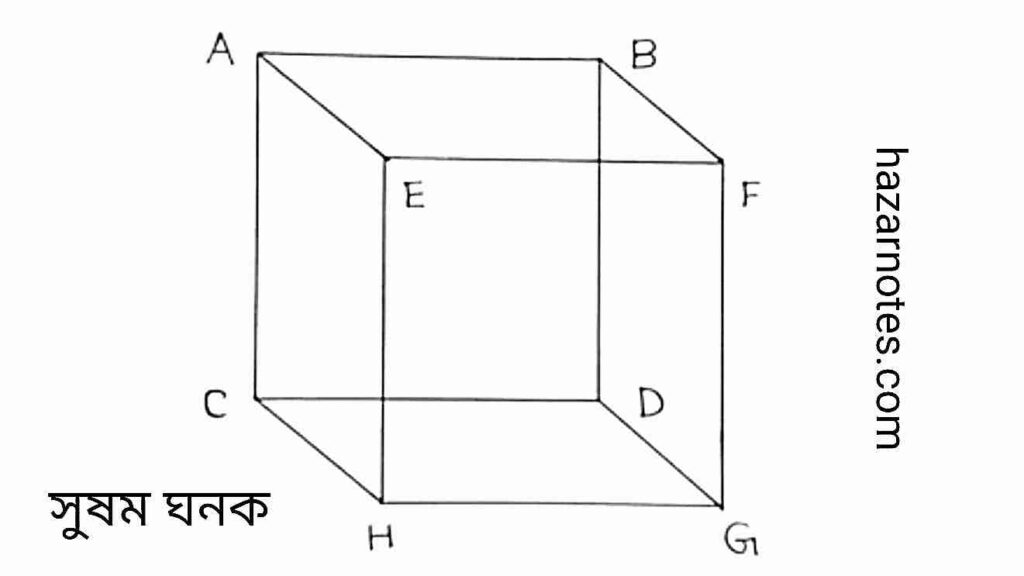
চিত্র : একটি সুষম ঘনকের ছয়টি তলই সমান আকারের বর্গক্ষেত্র দ্বারা গঠিত।
সুষমতা : এর প্রতিটি তল একটি সুষম বর্গক্ষেত্র এবং প্রতিটি শীর্ষবিন্দুতে তিনটি তল মিলিত হয়।
তলসংখ্যা : ৬টি।
(খ) একটি বৃত্ত এঁকে তার জ্যা, ব্যাস ও কেন্দ্র দেখাও। বৃত্তের ব্যাস ও ব্যাসার্ধের মধ্যে সম্পর্ক কী ? ৩+১
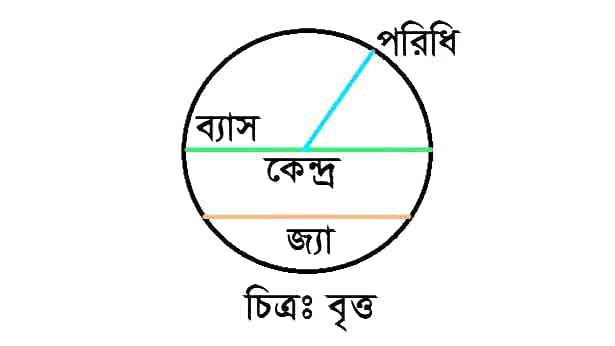
বৃত্তের ব্যাস ও ব্যাসার্ধের মধ্যে সম্পর্ক খুব সরল।
ব্যাসার্ধ (r) : বৃত্তের কেন্দ্র থেকে যে কোনো বিন্দু পর্যন্ত সরাসরি দূরত্ব।
ব্যাস (d) : বৃত্তের মধ্য দিয়ে সরাসরি লম্বভাবে গিয়ে দুই প্রান্তকে সংযুক্তকারী রেখা।
‘গ’ বিভাগ
৭। (ক) ১১, ১৭, ২৩, _____। পরের সংখ্যাটি কত ? ১
সমাধান :
১৭ − ১১ = ৬
২৩ − ১৭ = ৬
দেখা যাচ্ছে পার্থক্য ৬, এটি একটি সমান্তরাল ধারা।
পরের সংখ্যা = ২৩ + ৬ = ২৯
উত্তরঃ ২৯
(খ) টোপরের চিত্রটি আঁকো। ১
📌পঞ্চম শ্রেণি ইউনিট টেস্ট প্রশ্নপত্র Click Here
📌পঞ্চম শ্রেণি ইংরেজি প্রশ্নোত্তর Click Here
📌পঞ্চম শ্রেণি বাংলা প্রশ্নোত্তর Click Here
